从网络上看到下面一道题:
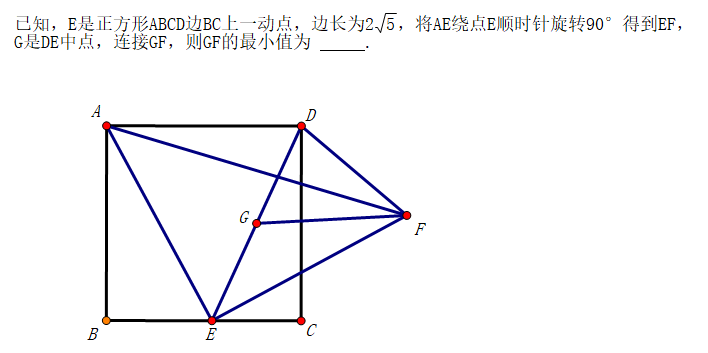
注意到点G和点F都是动点,设法进行转换。
由于存在中点,最直观的想法是构造出中位线。
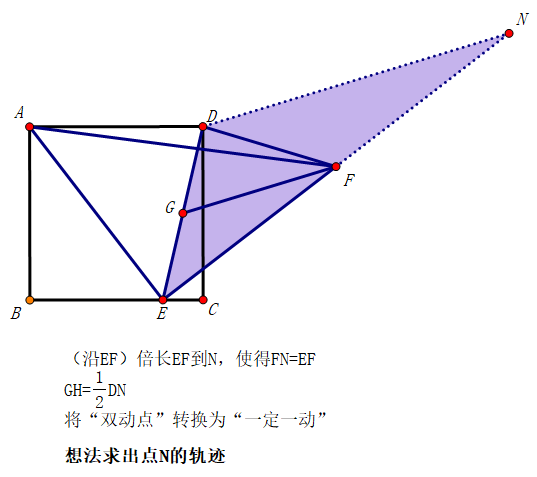
可以猜测出点N的轨迹为直线,如何确定?
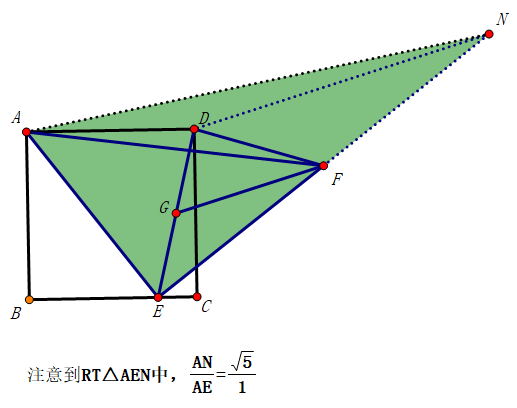
这个RT△是变化的,但有两条直角边存在固定倍数关系,很特殊。
想法构造出一个确定的类似RT△。
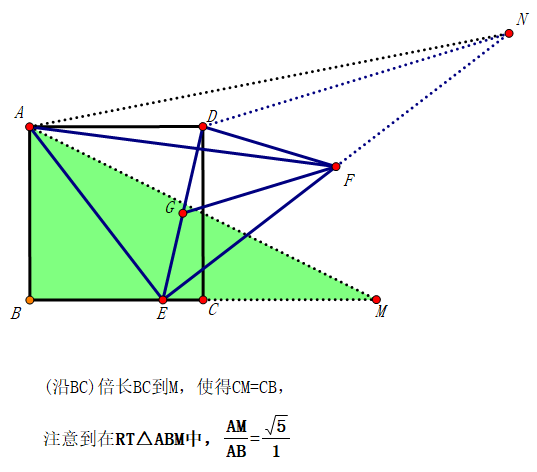
这个三角形是确定的!!!
不难证明图中两个三角形相似:
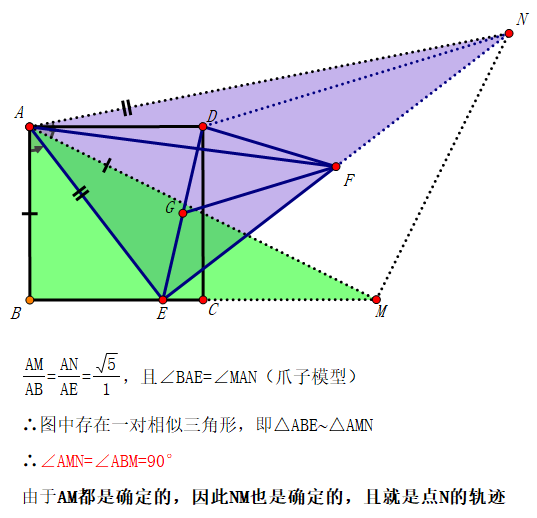
将△ABM绕定点A进行旋转,且放大,得到△AMN
实际上就是将△ABM绕定点A进行旋转,且放大,得到△AMN,
从而确定了点N的轨迹:垂直于确定线段AM的直线(线段)
问题转换为点到直线的距离。
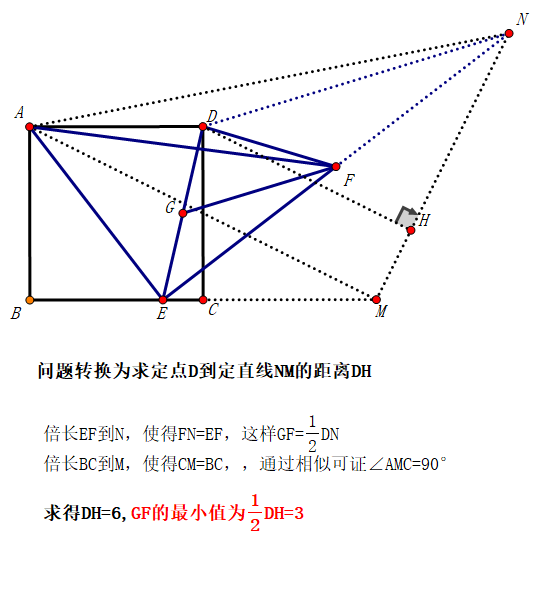
小结:瓜豆原理的构造是事先设定好的。首先要找出其特点,本题中的特点是两条直角之比为1:2,那么就想法构造出一个确定的类似直角三角形。然后通过SAS,得到相似形,进行倒角,从而确定动点轨迹。

